La ecuación de la elongación o ecuación de la posición o ecuación del movimiento (x ó y) de una partícula que describe un MAS, viene dada por:
Donde:
·
- A es la amplitud del movimiento es decir, el máximo desplazamiento de la partícula de su posición de equilibrio. Se expresa en metros (m) en el SI.
- ω es la frecuencia angular del movimiento. Se expresa en rad·s-1 en el SI
A la expresión (ω·t + ϕ0) se conoce como FASE del movimiento, y es un ángulo medido en radianes en el SI.
A ϕ0 se le denomina FASE INICIAL, y es el valor de la fase
en el instante t = 0. El valor de la fase inicial depende de las condiciones iníciales
del movimiento, es decir, de la posición y de la velocidad de la partícula en
el instante inicial. Así:
o
Si x (t =
0) = 0, es decir, si en el instante inicial la partícula se encuentra en la
posición de equilibrio, la ecuación del movimiento será una de estas dos:
x (t) = A·sen (ω·t) ó x (t) = A·sen (ω·t + π)
La primera ecuación indicaría que la partícula se encuentra inicialmente
en la posición de equilibrio y moviéndose hacia la parte positiva de la
trayectoria (velocidad inicial positiva), y la segunda que se mueve hacia la
parte negativa de la trayectoria (velocidad inicial negativa)
o
Si x (t =
0) = A, es decir, si en el instante inicial la partícula se encuentra en el
extremo positivo de la trayectoria, la ecuación será:
x (t) = A·sen (ω·t + π/2) = A·cos (ω·t)
o
Si x (t =
0) = -A, es decir, si en el instante inicial la partícula se encuentra en el
extremo negativo de la trayectoria, la ecuación será:
x (t) = A·sen (ω·t + 3π/2) = -A·cos (ω·t)
·
Observaciones a la ecuación de la posición
La ecuación también se puede expresar con la
función coseno, pero, la fase inicial de la función seno es diferente de la de
la función coseno para describir la misma situación inicial.
3.2 Velocidad de
vibración
La ecuación de la velocidad se determina derivando la
posición con respecto al tiempo. Tomando para ésta la ecuación resulta:
o
Observaciones a la ecuación de la
velocidad
-
El valor máximo de la velocidad es A·ω, y se
alcanza en aquellos instantes de tiempo para los que cos (ω·t + ϕ0) = ±1.
-
La velocidad alcanza su valor máximo cuando la
partícula pasa por la posición de equilibrio, x = 0.
3.3 Aceleración de
vibración
La ecuación de la aceleración se determina derivando la
velocidad con respecto al tiempo. Tomando para ésta la ecuación resulta:
o
Observaciones a la ecuación de la
aceleración
-
El valor máximo de la aceleración es A·ω2, y se
alcanza en aquellos instantes de tiempo para los que sen (ω·t + ϕ0) = ±1.
-
La aceleración máxima se alcanza en los extremos
de la trayectoria.
-
Se puede comprobar fácilmente que la aceleración
de un MAS es directamente proporcional a la posición pero de signo contrario:
Gráficas de la elongación (x), velocidad (v) y aceleración (a)
Podemos construir una tabla de
valores y representar gráficamente la posición, velocidad y aceleración para
una partícula con MAS. Se ha considerado el caso en el que el oscilador inicia
el movimiento en la posición de equilibrio con velocidad positiva, es decir ϕ0
= 0.
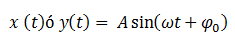





Publicar un comentario