La fuerza ejercida sobre un oscilador armónico y que cumple
la ley de Hooke, es conservativa, de lo que se deduce que la energía mecánica
(total) del oscilador se mantiene constante a lo largo de las distintas
oscilaciones.
Esto quiere decir que
en cada oscilación se produce una continua transformación de energía potencial
elástica en energía cinética.
Veamos las
expresiones de dichas energías tanto en función del tiempo como en función de
la posición.
Un cuerpo que
describe un MAS tiene energía cinética y energía potencial elástica
Energía cinética
La energía cinética de un oscilador armónico vale:
donde m es la masa del oscila+dor y v el valor de su
velocidad instantánea. Tomando la ecuación resulta:
En los extremos de la trayectoria la energía cinética vale 0
puesto que allí la partícula tiene velocidad 0. La energía cinética de la
partícula es máxima cuando pasa por el centro de la trayectoria, puesto que en
ese punto la velocidad es máxima, y vale:
Energía potencial
elástica
La energía potencial elástica de un oscilador armónico
sujeto a un muelle de constante K tiene la expresión:
donde x es la posición del oscilador con respecto a su
posición de equilibrio. Tomando la ecuación resulta:
En el centro de la trayectoria la energía potencial es 0,
puesto que en este punto la elongación es nula. En los extremos de la trayectoria
la energía potencial elástica de un oscilador armónico es máxima, puesto que en
ellos la elongación es máxima, y vale:
Que como
vemos coincide con la energía cinética máxima.
Energía mecánica
Si el
movimiento es no amortiguado, es decir, ausencia de rozamiento, entonces no
habría trabajo de fuerzas no conservativas y se cumpliría el PCEM, es decir, la
energía mecánica de la partícula permanecería constante en cualquier punto de
la trayectoria y en las sucesivas oscilaciones.
Esto quiere
decir que en cada oscilación se produce una continua transformación o
intercambio de energía potencial elástica en energía cinética y viceversa.
Como la
energía mecánica es la suma de la energía cinética y la energía potencial
elástica del oscilador. Así, al realizar dicha suma con las ecuaciones y
resulta:
con la que
se comprueba que la energía mecánica del oscilador es constante una vez fijados
los valores de la constante recuperadora, K, y la amplitud, A.
Gráfica energética del oscilador
armónico
En esta
gráfica se han representado las variaciones de energía cinética y potencial del
oscilador armónico a lo largo de una oscilación en función de la posición x. En
ella se observa cómo se produce una transformación continua de una forma de
energía en otra, de forma que la energía mecánica se mantiene constante.
Podemos
destacar en la gráfica que hay dos puntos simétricos a un lado y otro de la
posición de equilibrio, en los que la partícula tiene la misma energía cinética
que potencial, y que podemos localizar del modo siguiente:
que como
observamos son puntos que se encuentran mas cerca de los extremos que del
centro de la trayectoria.
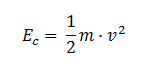

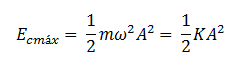





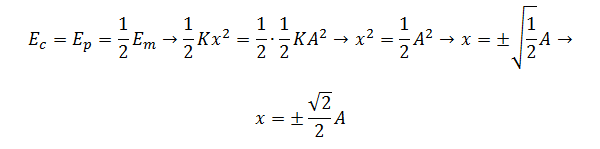
Publicar un comentario